数据结构学习笔记：二维树状数组

2023-7-14

简介

二维树状数组，其实就是原先一维的树状数组上的每个点变成了一个树状数组，层层 lowbit 操作维护了一个矩形。简单来说，我们现在操作的就是对一个二维矩阵进行类似于树状数组的操作（即使二维树状数组不常用，但它省空间啊）。

const int N = 2e3 + 10;
int bit[N][N], n, m;

操作

我们考虑一维树状数组维护区间是怎么维护的。

void add(int x, int d) {
    for (int i = x; i <= n; i += i & -i) {
        bit[i] += d;
    }
}

实际上，我们在进行单点操作的时候，考虑的是修改这个位置后有多少位置会被影响到。显然，我们可以通过i += i & -i的方式，逆推原本位置被树状数组所管理的区间内。对于二维树状数组，我们实际上进行的也是一模一样的操作。但是这次不同，如果一维树状数组维护的是一个一维的数列，那么二维树状数组就是维护了一个一个二维的矩阵了。

我们现在考虑的是这个位置修改后，会影响到几个矩阵内的值。当然，上面已经提到过，二维树状数组其实是一个树状数组套树状数组，也就是每个节点都是一个树状数组，因此，我们在进行修改操作的时候，对于第一维的树状数组，我们要考虑修改这个位置的树状数组会影响到多少个位置的树状数组，进入到第二维时考虑的就是这个位置修改后会影响到多少个位置。可以发现，这样的操作后其实就是修改了一个一个的小矩形了，总的单次修改的时间复杂度为 $O (\log n \log m)$ 。

void add(int x, int y, int d) {
    for (int i = x; i <= n; i += i & -i) {
        for (int j = y; j <= m; j += j & -j) {
            bit[i][j] += d;
        }
    }
}

那么对于查询操作呢？也是一样的道理。对于一维树状数组，我们要查询的，是 $[1, x]$ 范围内的区间，也就是前缀和。

int query(int x) {
    int ret = 0;
    for (int i = x; i > 0; i -= i & -i) {
        ret += bit[x];
    }
    return ret;
}

我们已经提到过，单点修改操作的本质其实是跟一维树状数组是一样的，那么查询操作也是同理，依然是考虑有多少个小矩形要加。当然，这次查询的，就是二维前缀和了，时间复杂度为 $O (\log x \log y)$ 。

int query(int x, int y) {
    int ret = 0;
    for (int i = x; i > 0; i -= i & -i) {
        for (int j = y; j > 0; j -= j & -j) {
            ret += bit[i][j];
        }
    }
    return ret;
}

单点加，区间查询

LOJ #133. 二维树状数组 1：单点修改，区间查询

给出一个 $n \times m$ 的零矩阵 $A$ ，你需要完成如下操作：

$1 x y k$ ：表示元素 $A_{x, y}$ 自增 $k$ ；
$2 a b c d$ ：表示询问左上角为 $(a, b)$ ，右下角为 $(c, d)$ 的子矩阵内所有数的和。

在上面的单点操作我们已经提到过了，二维树状数组的单点操作跟一维树状数组是一样的，因此我们可以直接加上就可以了。

对于区间查询，我们可以仔细思考我们使用二维树状数组实际上维护了什么。实际上，我们利用二维树状数组，维护的是一个二维的差分数组，查询的时候查的是这个二位差分数组的前缀和。所以，如果我们需要查询左上角为 $(x_{1}, y_{1})$ ，右下角为 $(x_{2}, y_{2})$ 的子矩阵内所有数的和，那么我们可以像前缀和数组一样利用容斥原理算出这个小矩形的和。

$a n s = S_{x_{2}, y_{2}} - S_{x_{1} - 1, y_{2}} - S_{x_{2}, y_{1} - 1} + S_{x_{1} - 1, y_{1} - 1}$

所以，我们执行查询操作的时候应该为query(x2,y2)-query(x1-1,y2)-query(x2,y1-1)+query(x1-1,y1-1)。

#include <bits/stdc++.h>
using namespace std;

using ll = long long;

int main() {
    std::cin.tie(nullptr)->sync_with_stdio(false);
    int n, m;
    cin >> n >> m;
    vector<vector<ll>> bit(n + 1, vector<ll>(m + 1));
    auto add = [&](int x, int y, ll d) {
        for (int i = x; i <= n; i += i & -i) {
            for (int j = y; j <= m; j += j & -j) {
                bit[i][j] += d;
            }
        }
    };
    auto query = [&](int x, int y) {
        ll ret = 0;
        for (int i = x; i; i -= i & -i) {
            for (int j = y; j; j -= j & -j) {
                ret += bit[i][j];
            }
        }
        return ret;
    };
    int opt;
    while (cin >> opt) {
        if (opt == 1) {
            int x, y, d;
            cin >> x >> y >> d;
            add(x, y, d);
        } else {
            int x1, y1, x2, y2;
            cin >> x1 >> y1 >> x2 >> y2;
            cout << query(x2, y2) - query(x1 - 1, y2) - query(x2, y1 - 1) + query(x1 - 1, y1 - 1) << '\n';
        }
    }
}

区间加，单点查询

LOJ #134. 二维树状数组 2：区间修改，单点查询

给出一个 $n \times m$ 的零矩阵 $A$ ，你需要完成如下操作：

$1 a b c d k$ ：表示询问左上角为 $(a, b)$ ，右下角为 $(c, d)$ 的子矩阵内所有数都自增加 $k$ ；
$2 x y$ ：表示询问元素 $A_{x, y}$ 的值。

现在我们的需求又变了，要修改的是一个区间，但是仅仅是一个单点查询的功能。

我们考虑单点查询的问题。还记得上一题吗？树状数组能够查询的，是一个位置的前缀和。因此，我们这边的单点查询，查询的依然是一个前缀和。什么玩意的前缀和是我们要的答案呢？当然是二维差分数组了。（下面的 $a$ 是原数组， $d$ 是差分数组）

$a_{n, m} = \sum_{i = 1}^{n} \sum_{j = 1}^{m} d_{i, j}$

因此，我们的目标是维护一个二维差分数组，用二维树状数组维护一个二维差分数组。

但是区间修改操作呢？比如这里的区间增加操作。因为我们现在的二维树状数组维护的是原数组的二维差分数组，因此，我们类似于修改差分数组一样，单点修改二维树状数组，依然用的是容斥原理。

#include <bits/stdc++.h>

using ll = long long;

int main() {
    std::cin.tie(nullptr)->sync_with_stdio(false);
    int n, m;
    std::cin >> n >> m;
    std::vector bit(n + 1, std::vector<ll>(m + 1));
    auto add = [&](int x, int y, ll d) {
        for (int i = x; i <= n; i += i & -i) {
            for (int j = y; j <= m; j += j & -j) {
                bit[i][j] += d;
            }
        }
    };
    auto query = [&](int x, int y) {
        ll ret = 0;
        for (int i = x; i; i -= i & -i) {
            for (int j = y; j; j -= j & -j) {
                ret += bit[i][j];
            }
        }
        return ret;
    };
    int opt;
    while (std::cin >> opt) {
        if (opt == 1) {
            int x1, y1, x2, y2, d;
            std::cin >> x1 >> y1 >> x2 >> y2 >> d;
            add(x1, y1, d);
            add(x1, y2 + 1, -d);
            add(x2 + 1, y1, -d);
            add(x2 + 1, y2 + 1, d);
        } else {
            int x, y;
            std::cin >> x >> y;
            std::cout << query(x, y) << '\n';		
        }
    }
}

区间加，区间查询

LOJ #135. 二维树状数组 3：区间修改，区间查询

给定一个大小为 $N \times M$ 的零矩阵，直到输入文件结束，你需要进行若干个操作，操作有两类：

1 a b c d x，表示将左上角为 $(a, b)$ ，右下角为 $(c, d)$ 的子矩阵全部加上 $x$ ；
2 a b c d，表示询问左上角为 $(a, b)$ ，右下角为 $(c, d)$ 为顶点的子矩阵的所有数字之和。

现在我们的目标又上一层台阶了，我们不仅是要进行区间加法，还要区间查询原数组的区间和，而不是差分数组的前缀和。但是，我们的树状数组维护的依然是一个差分数组，而不是线段树那样的直观（当然，这道题如果想要用二维线段树的话依然会MLE）。

我们用 $s$ 记为原数组的前缀和， $a$ 记为原数组， $d$ 记为差分数组。

现在，我们要开始考虑单个位置 $d_{k, l}$ 对前缀和 $s_{n, m}$ 能够提供多少贡献。我们可以知道， $a_{i, j} = \sum_{k = 1}^{n} \sum_{l = 1}^{m} d_{k, l}$ ，也就是说，单个位置的 $d_{k, l}$ ，对于原数组的贡献只有一个。

现在我们来前缀和： $s_{n, m} = \sum_{i = 1}^{n} \sum_{j = 1}^{m} a_{i, j} = \sum_{i = 1}^{n} \sum_{j = 1}^{m} \sum_{k = 1}^{i} \sum_{l = 1}^{j} d_{k, l}$ 。对于单个 $a_{i, j}$ ，它对前缀和的贡献依然是一个，但是如果是 $d_{i, j}$ 的话，我们依然可以利用容斥原理来考虑它的贡献。我们可以参考下面的图进行计算。

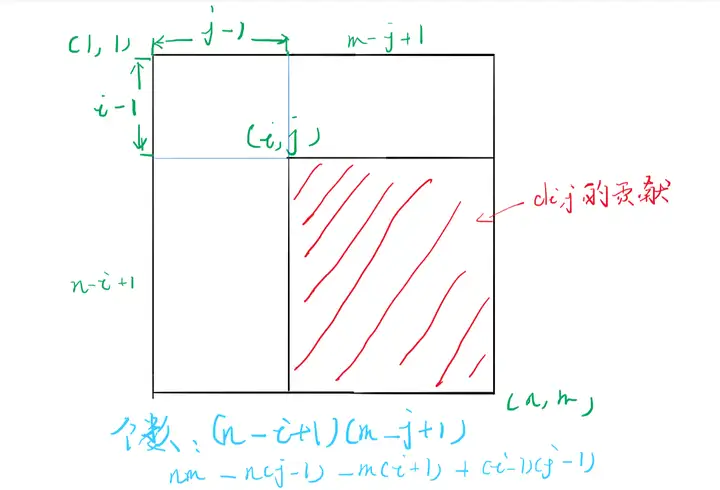
可以发现，对于 $d_{i, j}$ 这个位置，它对于前 $i - 1$ 行是不存在贡献的，对于前 $j - 1$ 列也是没有任何贡献的，而在左上角 $(i, j)$ 到右下角 $(n, m)$ 的矩形，它是有贡献的，贡献了 $(n - i + 1) (m - j + 1) d_{i, j}$ 。也就是说，现在我们的前缀和公式和差分公式可以更直接的联系在一起了。

$s_{n, m} = \sum_{i = 1}^{n} \sum_{j = 1}^{m} (n - i + 1) (m - j + 1) d_{i, j}$

但是，我们还需要将 $n, m$ 提出来。实际上，我们更刚刚所考虑的，都是在查询 $s_{n, m}$ 这个前缀和，也就是 $(n, m)$ 这个位置的前缀和（注意这不是题目中的 $n, m$ ，而是查询的 $x, y$ ），因此，我们无法将这两个参数代入维护，因为这两个参数的变化是没规律的。但是如果我们将其稍微化简一下后会发现，整个式子中的 $n, m$ 其实就可以提出了，具体像下面的式子。

$\begin{aligned} s_{n, m} & = \sum_{i = 1}^{n} \sum_{j = 1}^{m} a_{i, j} \\ = \sum_{i = 1}^{n} \sum_{j = 1}^{m} \sum_{k = 1}^{i} \sum_{l = 1}^{j} d_{k, l} \\ = \sum_{i = 1}^{n} \sum_{j = 1}^{m} (n - i + 1) (m - j + 1) d_{i, j} \\ = \sum_{i = 1}^{n} \sum_{j = 1}^{m} [n m - m (i - 1) - n (j - 1) + (i - 1) (j - 1)] b_{i, j} \\ = n m \sum_{i = 1}^{n} \sum_{j = 1}^{m} d_{i, j} - m \sum_{i = 1}^{n} \sum_{j = 1}^{m} (i - 1) d_{i, j} - n \sum_{i = 1}^{n} \sum_{j = 1}^{m} (j - 1) d_{i, j} + \sum_{i = 1}^{n} \sum_{j = 1}^{m} (i - 1) (j - 1) d_{i, j} \end{aligned}$

现在可以看到，我们实际上只需要维护 $d_{i, j}, (i - 1) d_{i, j}, (j - 1) d_{i, j}, (i - 1) (j - 1) d_{i, j}$ 就可以了。当我们要查询 $(x, y)$ 位置的时候，只需要将对应系数带上就可以了。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

const int N = 2050;
int n, m;
ll a[N][N], b[N][N], c[N][N], d[N][N];

void add(int x, int y, ll v) {
    for (int i = x; i <= n; i += i & -i) {
        for (int j = y; j <= m; j += j & -j) {
            a[i][j] += v;
            b[i][j] += (x - 1) * v;
            c[i][j] += (y - 1) * v;
            d[i][j] += (x - 1) * (y - 1) * v;
        }
    }
}
ll query(int x, int y) {
    ll ret = 0;
    for (int i = x; i > 0; i -= i & -i) {
        for (int j = y; j > 0; j -= j & -j) {
            ret += x * y * a[i][j]
                - y * b[i][j]
                - x * c[i][j]
                + d[i][j];
        }
    }
    return ret;
}

int main() {
    std::cin.tie(nullptr)->sync_with_stdio(false);
    cin >> n >> m;
    int opt;
    while (cin >> opt) {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        if (opt == 1) {
            ll v;
            cin >> v;
            add(x1, y1, v);
            add(x1, y2 + 1, -v);
            add(x2 + 1, y1, -v);
            add(x2 + 1, y2 + 1, v);
        } else {
            cout << 
                query(x2, y2) 
                - query(x1 - 1, y2) 
                - query(x2, y1 - 1) 
                + query(x1 - 1, y1 - 1)
            << '\n';
        }
    }
}

THE END

Transformer作者：指令型智能体的构建之法

<<上一篇

java编程学习：数组的基本用法

下一篇>>