HTML5中手势原理分析与数学知识的实践

2023-7-6

触控屏的时代，人性化的手势操作已经深入了我们生活的每个部分。现代应用越来越重视与用户的交互及体验，手势是最直接且最为有效的交互方式，一个好的手势交互，能降低用户的使用成本和流程，大大提高了用户的体验。

拖动: drag
双指缩放: pinch
双指旋转: rotate
单指缩放: singlePinch
单指旋转: singleRotate
长按: tap
滑动: swipe

所有的手势都是基于浏览器原生事件touchstart, touchmove, touchend, touchcancel进行的上层封装，因此封装的思路是通过一个个相互独立的事件回调仓库handleBus，然后在原生touch事件中符合条件的时机触发并传出计算后的参数值，完成手势的操作。

基础数学知识

常见的坐标系属于线性空间，或称向量空间 (Vector Space)。这个空间是一个由点 (Point) 和向量 (Vector) 所组成集合；

1.点(Point)

可以理解为我们的坐标点,例如原点O(0,0),A(-1,2)，通过原生事件对象的touches可以获取触摸点的坐标，参数index代表第几接触点；

// 获取触摸点
function getPoint(ex,index){
    return {
        x:Math.round(ev.touches[index].pageX),
        y:Math.round(ev.touches[index].pageY)
    }
}

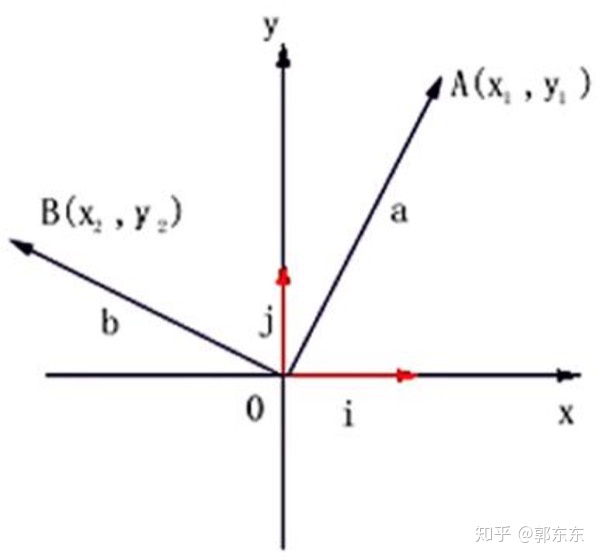
2.向量(Vector)

向量是坐标系中一种既有大小也有方向的线段，例如由原点O(0,0)指向点A(1,1)的箭头线段，称为向量a，则a=(1-0,1-0)=(1,1);

//获取两个点的向量
function getVector(p1, p2) {
    let x = Math.round(p1.x - p2.x)
    let y = Math.round(p1.y - p2.y);
    return {
        x,
        y
    };
}

如下图所示，其中i与j向量称为该坐标系的单位向量，也称为基向量，我们常见的坐标系单位为1,即i=(1,0)；j=(0,1)；

图例

3.向量模

代表向量的长度，记为|a|，是一个标量，只有大小，没有方向;

几何意义代表的是以x,y为直角边的直角三角形的斜边，通过勾股定理进行计算；

// 获取某个向量的模
function getLength(v1) {
    return Math.sqrt(v1.x * v1.x + v1.y * v1.y);
}

4.向量的数量积

向量同样也具有可以运算的属性，它可以进行加、减、乘、数量积和向量积等运算，接下来就介绍下我们使用到的数量积这个概念，也称为点积，被定义为公式：

当a=(x1,y1),b=(x2,y2)，则a·b=|a|·|b|·cosθ=x1·x2+y1·y2；

5.共线定理

共线，即两个向量处于平行的状态，当a=(x1,y1),b=(x2,y2)，则存在唯一的一个实数λ，使得a=λb，代入坐标点后，可以得到 x1·y2= y1·x2;

因此当x1·y2-x2·y1>0 时，既斜率 ka > kb ，所以此时b向量相对于a向量是属于顺时针旋转，反之，则为逆时针；

6.旋转角度

通过数量积公式我们可以推到求出两个向量的夹角：

cosθ=(x1·x2+y1·y2)/(|a|·|b|);

然后通过共线定理我们可以判断出旋转的方向，函数定义为：

/* 获取向量的夹角 */
// 判断方向，顺时针为 1 ，逆时针为 -1;
function getAngle(v1, v2) {

    let direction = v1.x * v2.y - v2.x * v1.y > 0 ? 1 : -1;
    let len1 = getLength(v1);
    let len2 = getLength(v2);
    let mr = len1 * len2;
    let dot, r;

    if (mr === 0) return 0;

    // 通过数量积公式可以推导出:
    // cos =(x1 *x2 +y1*y2)/(lal * Ib1);

    dot = v1.x * v2.x + v1.y * v2.y;
    r = dot / mr;

    if (r > 1) r = 1;
    if (r < -1) r = -1;

    // 解值并结合方向转化为角度值;
    // 180 / Math.PI
    return Math.acos(r) * direction;

}

7.矩阵与变换

由于空间最本质的特征就是其可以容纳运动，因此在线性空间中，用向量来刻画对象，而矩阵便是用来描述对象的运动；

而矩阵是如何描述运动的呢?

通过一个坐标系基向量便可以确定一个向量，例如 a=(-1,2),我们通常约定的基向量是 i = (1,0) 与 j = (0,1) ；因此:

a = -1i + 2j = -1(1,0) + 2(0,1) = (-1+0,0+2) = (-1,2);

而矩阵变换的，其实便是通过矩阵转换了基向量，从而完成了向量的变换；

例如上面的栗子，把a向量通过矩阵(1,2,3,0)进行变换，此时基向量i由 (1,0)变换成(1,-2)与j由(0,1)变换成(3,0),沿用上面的推导，则

a = -1i + 2j = -1(-1,2) + 2(3,0) = (5,-2);

其实向量与坐标系的关联不变(a = -1i+2j)，是基向量引起坐标系变化，然后坐标系沿用关联导致了向量的变化；

结合代码

1.实际例子

CSS 的transform等变换便是通过矩阵进行的，我们平时所写的 translate/rotate 等语法类似于一种封装好的语法糖，便于快捷使用，而在底层都会被转换成矩阵的形式。例如 transform:translate(-30px,-30px)编译后会被转换成 transform : matrix(1,0,0,1,30,30);

通常在二维坐标系中，只需要 2X2 的矩阵便足以描述所有的变换了，但由于CSS是处于3D环境中的，因此CSS中使用的是 3X3 的矩阵，表示为：

矩阵

其中第三行的0,0,1代表的就是z轴的默认参数。这个矩阵中，(a,b) 即为坐标轴的 i基，而(c,d)既为j基,e为x轴的偏移量,f为y轴的偏移量;因此上栗便很好理解，translate并没有导致i，j基改变，只是发生了偏移，因此translate(-30px,-30px) ==> matrix(1,0,0,1,30,30)~

所有的transform语句，都会发生对应的转换，如下：

// 发生偏移，但基向量不变；
transform:translate(x,y) ==> transform:matrix(1,0,0,1,x,y)

// 基向量旋转；
transform:rotate(θdeg)==> transform:matrix(cos(θ·π/180),sin(θ·π/180),-sin(θ·π/180),cos(θ·π/180),0,0)

// 基向量放大且方向不变；
transform:scale(s) ==> transform:matrix(s,0,0,s,0,0)

translate/rotate/scale等语法十分强大，让我们的代码更为可读且方便书写，但是matrix有着更强大的转换特性，通过matrix，可以发生任何方式的变换，例如常见的镜像对称，transform:matrix(-1,0,0,1,0,0);

2.MatrixTo

transform:matrix(1.41421, 1.41421, -1.41421, 1.41421, -50, -50);

通过矩阵计算出实际缩放的比例和旋转的角度，矩阵前4个参数会同时受到rotate和scale的影响，具有两个变量，因此需要通过前两个参数根据上面的转换方式列出两个不等式：

cos(θ·π/180)*s=1.41421;
sin(θ·π/180)*s=1.41421;

将两个不等式相除，即可求出θ和s，函数如下：

// 转换矩阵
function matrixTo(matrix) {
    
    // 解析 matrix 字符串，分割成数组;
    let arr = (matrix.replace('matrix(',).replace(')', '')).split(',');
    // 根据不等式计算出 rotate 和 scale;
    let cos = arr[0], sin = arr[1], tan = sin / cos;
    let rotate = Math.atan(tan) * 180 / Math.PI;
    let scale = cos / (Math.cos(Math.PI / 180 * rotate));

    return {
        x: parseInt(arr[4]),
        y: parseInt(arr[5]),
        scale,
        rotate
    }
}

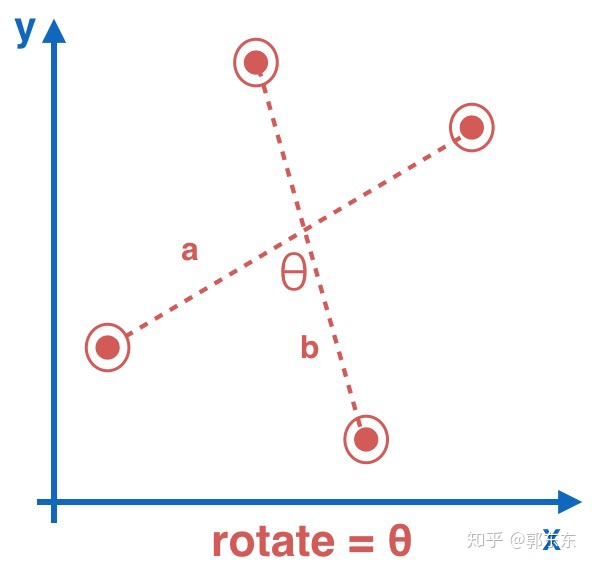
3.Rotate(双指旋转)

初始时双指向量a，旋转到b向量，θ代表旋转的角度，因此只要通过上面构建的getAngle函数，便可求出旋转的角度：

双指旋转

// a向量；
let vector1 = getVector(secondPoint, startPoint);
// b向量；
let vector2 = getVector(curSecPoint, curPoint);

// 触发事件;
this._eventFire('rotate', {
    delta: {
        rotate: getAngle(vector1, vector2),
    },
    origin: ev,
});

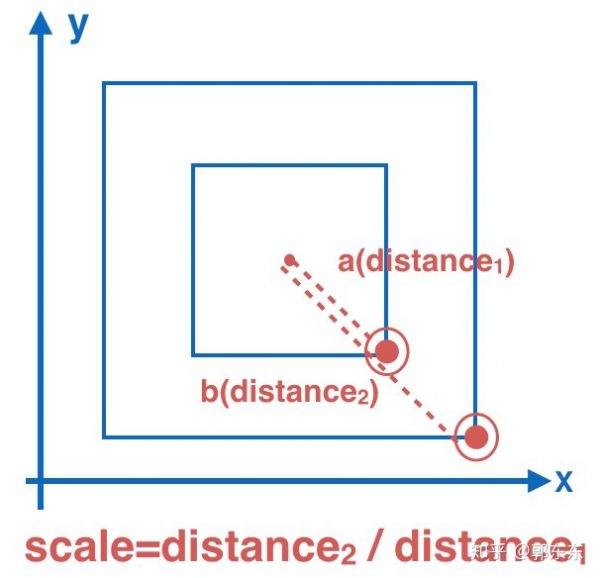
4.singleRotate(单指旋转)

单指旋转

// 获取初始向量与实时向量
let rotateV1 = getVector(startPoint, singleBasePoint);
let rotateV2 = getVector(curPoint, singleBasePoint);

// 通过 getAngle 获取旋转角度并触发事件；
this._eventFire('singleRotate', {
    delta: {
        rotate: getAngle(rotateV1, rotateV2),
    },
    origin: ev,
});

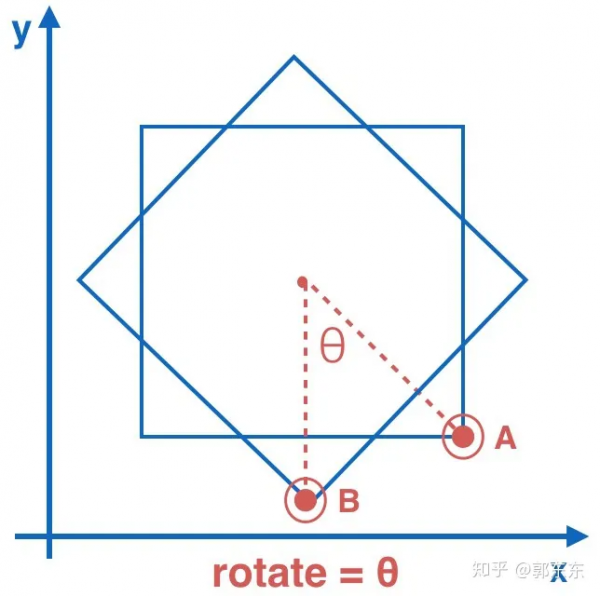
5.Pinch(双指缩放)

双指缩放

// touchstart中计算初始双指的向量模；
let vector1 = getVector(secondPoint, startPoint);
let pinchStartLength = getLength(vector1);

// touchmove中计算实时的双指向量模；
let vector2 = getVector(curSecPoint, curPoint);
let pinchLength = getLength(vector2);
this._eventFire('pinch', {
    delta: {
        scale: pinchLength / pinchStartLength,
    },
    origin: ev,
});

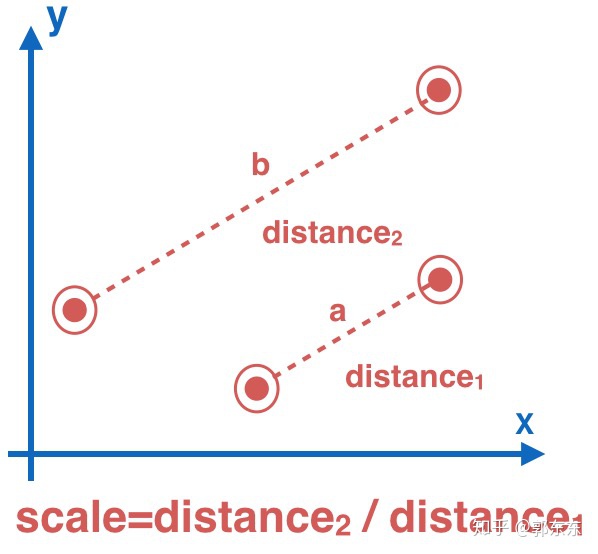
6.SinglePinch(单指缩放)

单指缩放

// 计算单指操作时的基准点，获取operator的中心点；
let singleBasePoint = getBasePoint(operator);

// touchstart 中计算初始向量模；
let pinchV1 = getVector(startPoint,singleBasePoint);
singlePinchStartLength = getLength(pinchV1);

// touchmove 中计算实时向量模；
pinchV2 = getVector(curPoint, singleBasePoint);
singlePinchLength = getLength(pinchV2);

// 触发事件；
this._eventFire('singlePinch', {
    delta: {
        scale: singlePinchLength / singlePinchStartLength,
    },
    origin: ev,
});

THE END

17款最好用的免费录制在线网课的软件工具

<<上一篇

xdebug、PHPSTORM 配置PHP 断点 DEBUG 相关配置

下一篇>>